Support de l'étude proposée
Depuis la version R18 (SP5) de CATIA V5, il est possible de réaliser des calculs éléments finis en présence de contact avec frottement. Jusque alors, la
prise en compte du frottement n’était pas possible. Mais le frottement est un phénomène non-linéaire qu’il complique fortement la résolution des problèmes de mécanique des structures. L’unicité de la solution n’est même pas prouvée !

Benchmark pour le calcul d’un problème de contact avec frottement (source : Thèse Laurent Champaney)
Modélisation du problème dans CATIA

Dans l’atelier d’analyse éléments finis, une condition de contact avec frottement est imposée entre les deux solides, en plus des conditions aux limites et chargements classiques.
Le maillage utilisé est régulier (taille de 0.5 mm) (solide déformable en orange, socle rigide en bleu).
Analyse statique : avec et sans frottement
Si l’on impose un contact sans frottement entre les deux solides, la solution est rapide à calculer (27 s d’attente devant la machine).
Si l’on impose un contact avec frottement (coefficient 1) entre les deux solides, la solution est beaucoup plus longue à calculer (10 min d’attente environ devant la machine).


Norme du champ de déplacement obtenu par le calcul EF sans (image de gauche) puis avec frottement (image de droite)
Comparaison avec des résultats de la littérature
On retrouve bien dans les résultats de la littérature la présence de trois zones distinctes :
- décollement d’une première zone : la pression de contact est nulle, et les efforts tangentiels également bien évidemment ;
- contact et glissement sur une seconde zone : les densités d’effort sont non nulles mais égales (puisque le coefficient de frottement est unitaire) ;
- contact et adhérence : les efforts tangentiels sont strictement inférieurs aux efforts normaux (multipliés par le coefficient de frottement qui est unitaire ici).

Evolution de la pression de contact et de la densité d’effort tangentiel le long de la zone de contact (source : Thèse Laurent Champaney)
Le tracé du champs de contraintes normales (nn) et tangentielles (nt) sur la zone de contact permet de tracer par la suite le même de graphique que celui qui nous sert de référence. Pour cela, il faut exporter les résultats de CATIA dans un fichier texte puis tracer les courbes avec un tableur. Les courbes obtenues (pour une série de point appartenant à un plan de coupe) sont fournies ci-dessous. Les résultats sont du bon ordre de grandeur, et on devine bien 3 zones. Mais lorsqu’il y a glissement, on n’a pas l’égalité parfaite des efforts normaux et tangentiels (coefficient de 1). Ce point est assez décevant.
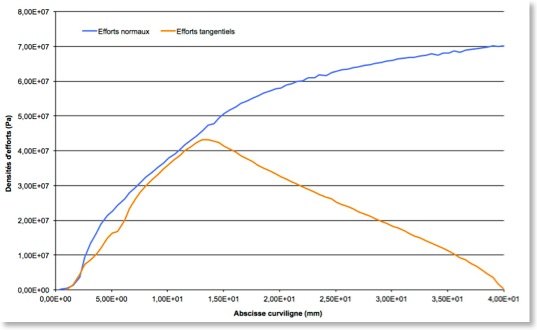
Evolution de la pression de contact et de la densité d’effort tangentiel le long de la zone de contact (Calcul CATIA V5)