Création de modèles éléments finis de type « poutre »

Objectifs

Certains problèmes peuvent être résolus rapidement en adoptant un modèle poutre. Dans ce cas, la géométrie sous jacente au modèle éléments finis est filaire et donc réalisée avec les ateliers WireFrame And Surface Design ou encore Generative Shape Design. Une fois l'atelier de calcul éléments finis ouvert à partir de cette géométrie, il faut créer le maillage, définir la section droite, puis le matériau de la poutre. Le reste du calcul (chargement, conditions aux limites) se fait classiquement.

Exemple élémentaire : une poutre

Dans cet exemple on cherche à modéliser puis simuler le comportement d'une poutre en statique.On vérifie notamment que l’on obtient bien comme flèche

à l’extrémité d’une poutre encastrée soumise à un chargement

Création de la géométrie filaire : Tutorial
Création du maillage, des propriétés poutre : Tutorial
Définition du cas d'analyse et post-traitement : Tutorial

Cas d'un treillis

On considère un treillis plan constitué de 11 poutres rigidement liées entre elles (un encastrement, et pas une articulation). Les triangles constitués par les poutres sont équilatéraux et de côté 1000/3 mm. La section de chaque poutre est de 12 mm x 4 mm. Pour le calcul, le treillis est en appui sur deux biellettes, elles même articulées par rapport au bâti.

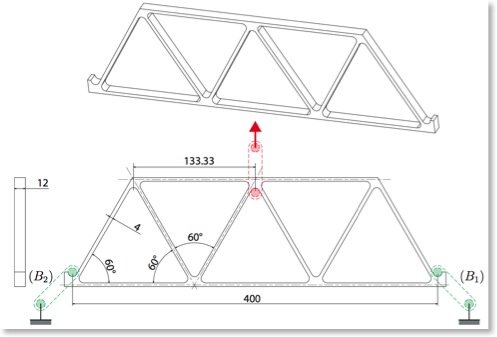
Un calcul basée la géométrie volumique peut bien entendu être mené, mais il conduit à un coût de calcul important par rapport à un modèle treillis simple. Le modèle treillis que l'on va réaliser est présenté ci-contre.

La géométrie du treillis est réalisée dans un atelier permettant de faire du filaire (au choix). Les grandes étapes de cette construction sont présentées dans quelques animations et résumées ci-dessous :

définir les points géométriques correspondant aux noeuds du treillis ; le treillis étant symétrique, tout comme les conditions aux limites et le chargement, on se contente des points A, B, C, D et H, milieu de [ED].
créer des polydroites passant par ces points : H,D,C,B,A puis A,D,B ; assembler ces deux géométries pour n'en faire plus qu'une seule et lui appliquer un matériau éventuellement (aluminium) : Tutorial
démarrer l'atelier d'analyse éléments finis, insérer un cas statique, puis mailler la structure à l'aide du mailleur poutre ; imposer une section rectangulaire de 12mmx4mm en sélectionnant comme géométrie d'orientation le plan contenant le treillis : Tutorial
imposer comme conditions aux limites : un déplacement imposé nul selon un axe incliné d'un angle donné en C, un déplacement axial et une rotation hors plan nulle en A et H (condition de symétrie), un déplacement hors plan nul partout de façon à bloquer le mouvement de corps rigide restant : Tutorial
imposer un chargement ponctuel au point A puis réaliser le calcul et le post-traitement : Tutorial

Une méthode analytique simple permet de valider ces résultats. On considère le même treillis, mais cette fois on suppose que les liaisons entre les barres sont des articulations. Le calcul analytique des sollicitations dans chaque barre est ainsi très simple à réaliser puisque le problème est par ailleurs isostatique. On choisit la convention suivante : les efforts des barres sur un noeud sont dirigés du centre de ce noeud vers l'extérieur, comme indiqué sur la figure ci-contre.

Si l'effort obtenu après résolution est positif, la barre sera donc sollicitée en traction et inversement. On note